Goal
Simplest embedding problem using Tensorflow Inspiried from this: http://matpalm.com/blog/2015/03/28/theano_word_embeddings/ https://colah.github.io/posts/2015-01-Visualizing-Representations/
https://colah.github.io/posts/2014-07-NLP-RNNs-Representations/
I first worked with embedding vectors in machine learning / neural
networks many years ago where we called them context vectors and used
them to do things like automatic text summarization, named entity
recognition, and semantic machine translation.
Embedding is powerful: word2vec, glove, neural image captioning, ...
Hinton started calling them thought vectors.
The basic idea is to embed objects that might not have much direct
relation to each other into a space where higher semantic meaning
might be more easily seen using simple operations like distance. An
example is English words. Looking in the dictionary the words "happen"
and "happy" occur right next to each other. However their meanings are
quite different; alphabetic distance isn't too useful when dealing
with word meanings. Wouldn't it be nice to embed those words in a
space where words with similar meanings are close together (viz:
synonyms happen==occur / happy==cheerful)....
================================
https://colah.github.io/posts/2015-01-Visualizing-Representations/
https://colah.github.io/posts/2014-07-NLP-RNNs-Representations/
I first worked with embedding vectors in machine learning / neural
networks many years ago where we called them context vectors and used
them to do things like automatic text summarization, named entity
recognition, and semantic machine translation.
Embedding is powerful: word2vec, glove, neural image captioning, ...
Hinton started calling them thought vectors.
The basic idea is to embed objects that might not have much direct
relation to each other into a space where higher semantic meaning
might be more easily seen using simple operations like distance. An
example is English words. Looking in the dictionary the words "happen"
and "happy" occur right next to each other. However their meanings are
quite different; alphabetic distance isn't too useful when dealing
with word meanings. Wouldn't it be nice to embed those words in a
space where words with similar meanings are close together (viz:
synonyms happen==occur / happy==cheerful)....
================================
The Setup
- Predict whether two objects (o and p) are "compatible" / should occur together or not. - Embed N arbitrary objects identified by integers into 2d (x,y) (so I can plot them) - Try learning a simple linear ordering "compatibility" function: - Make adjacent pairs compatible Prob(o,p)=1.0 : (o,p) = (0,1), (1,2), (4,5), ... - Make all others incompatible Prob(o,p)=0.0 : (o,p) = (0,2), (3,5), ... - Assume pairs are ordered so (o,p) -> p>o - Try a very simple learning network: Input: (o, p) (object integers) Embed: embedding(o) = 2d Computation: f(o,p) = single linear layer. input = [embedding(x), embedding(y)] output= logit for [1-P, P] where P is probability o,p are compatible Output: softmax of network output The key here is that when learning, gradients can be pushed back to the embedding vectors so they can be updated. It is _automatic_ in frameworks like Tensorflow. Source Code: https://github.com/michaelbrownid/simplest-embedding or simply simplest-embedding.python.txt The relevant parts are quite simple:
# input batchSize by two integer object numbers
inputData = tf.placeholder(tf.int32, [None,2])
# target is batchSize probability of compatible: [1-Prob(compat), Prob(compat)]
target = tf.placeholder(tf.float32, [None,2])
# this is the matrix of embedding vectors. rows=objects. cols=embedding. random [-1,1]
embedding = tf.Variable(tf.random_uniform([numObjects, embeddingSize], -1.0, 1.0))
# pull out the embedding vectors from integer ids
emap = tf.nn.embedding_lookup(embedding, inputData)
# reshape to feed pair of embedding points as single vector per datapoint
inputs = tf.reshape(emap , [-1, 2*embeddingSize])
# Set model to linear function to [1-p,p] 2d prediction vector
softmaxW = tf.Variable(tf.random_normal([2*embeddingSize,2],stddev=0.1), name="softmaxW")
softmaxB = tf.Variable(tf.random_normal([1,2], stddev=0.1), name="softmaxB")
logits = tf.matmul(inputs, softmaxW ) + softmaxB
probs = tf.nn.softmax(logits)
# cross entropy loss = \sum( -log(P prediction) of correct label)/N. Jensen's E(logX) < = logE(X).
cross = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits( logits, target))
# optimize
optimizer = tf.train.AdamOptimizer(learningRate).minimize(cross)
Note this is interesting because we will estimate both the embedding
and the linear discriminant function on the embedding simultaneously.
TODO: eliminate the linear function and use dot product with no
learned parameters.
================================
RESULT
Animate the embeddings and the decision boundries for the first 4 points (colors=black, red, green, blue) every 3 epochs of optimization for 1000 epochs total.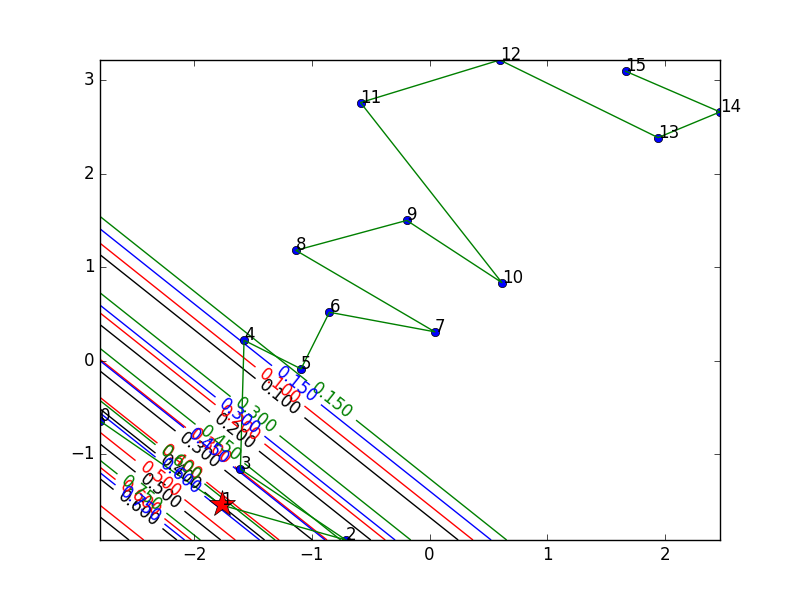
What experiment do you want to see?
Coverged1NotQuite
Converged2
current / 333
frame step
frame delay Smaller for faster animation!
Animate!
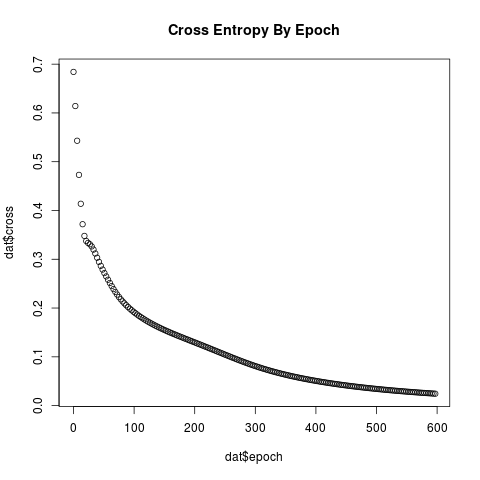
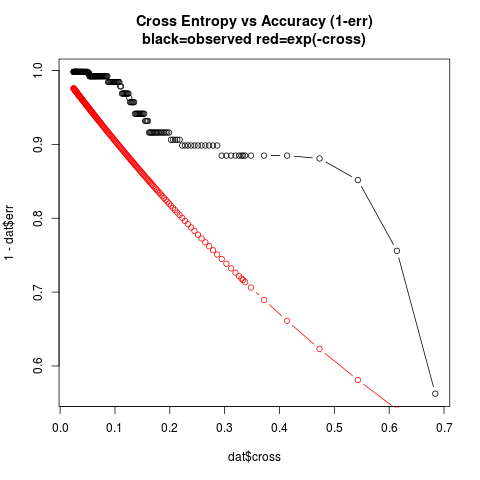 Jensen's Inequality relates the mean accuracy to mean cross-entropy.
Here $P$ is the probability assigned to the correct label and the
brackets are the expectation operator:
$$cross = < -\log P>$$
$$ -cross = (< \log P>) \leq (\log < P>)$$
$$ (< P>) \geq (\exp(-cross)) $$
This isn't too exciting but it is interesting to see the nice linear
chain that is learned from a number of pairwise examples. It reminds
me of the Hammersley-Clifford theorem where a joint density can be
factorized over cliques (Hammersley-Clifford theorem)
Jensen's Inequality relates the mean accuracy to mean cross-entropy.
Here $P$ is the probability assigned to the correct label and the
brackets are the expectation operator:
$$cross = < -\log P>$$
$$ -cross = (< \log P>) \leq (\log < P>)$$
$$ (< P>) \geq (\exp(-cross)) $$
This isn't too exciting but it is interesting to see the nice linear
chain that is learned from a number of pairwise examples. It reminds
me of the Hammersley-Clifford theorem where a joint density can be
factorized over cliques (Hammersley-Clifford theorem)
 It seems the ordering happens fairly quickly then the decision boundry
tightens up.
It is simple but interesting. Next it might be interesting to take ZIP
codes and embed them. First simply try to "learn"
ZIP->(latitude,longitude). Then try to pull out additional covariates
like median income, total population, ..., from the embedded vectors.
================================
It seems the ordering happens fairly quickly then the decision boundry
tightens up.
It is simple but interesting. Next it might be interesting to take ZIP
codes and embed them. First simply try to "learn"
ZIP->(latitude,longitude). Then try to pull out additional covariates
like median income, total population, ..., from the embedded vectors.
================================
